In the previous article, we have discussed Python Program to Check if a Pair with Given Product Exists in a Matrix
Given a square matrix and the task is to check whether the given matrix is a diagonally dominant matrix or not.
What is a matrix:
A matrix is a rectangular sequence of numbers divided into columns and rows. A matrix element or entry is a number that appears in a matrix.
Example:
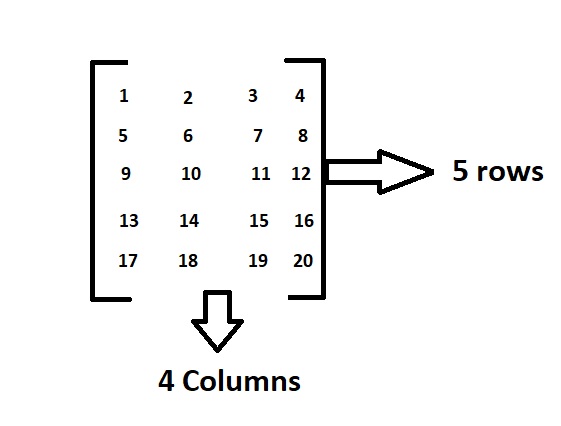
Above is the matrix which contains 5 rows and 4 columns and having elements from 1 to 20.
In this order, the dimensions of a matrix indicate the number of rows and columns.
Here as there are 5 rows and 4 columns it is called a 5*4 matrix.
Diagonally Dominant Matrix :
A square matrix is said to be diagonally dominating in mathematics if the magnitude of the diagonal entry in a row is greater than or equal to the sum of the magnitudes of all the other (non-diagonal) values in that row for each row of the matrix.
Examples:
Example1:
Input:
Given Matrix : 5 1 3 2 7 1 4 0 9
Output:
Yes, the given matrix is a diagonally dominant matrix
Example2:
Input:
Given Matrix : 1 3 5 2 4 6 7 8 9
Output:
No, the given matrix is not a diagonally dominant matrix
Program to Check Diagonally Dominant Matrix in Python
Below are the ways to check whether the given matrix is a diagonally dominant matrix or not in python:
Method #1: Using For Loop (Static Input)
Approach:
- Give the matrix as static input and store it in a variable.
- Calculate the number of rows of the given matrix by calculating the length of the nested list using the len() function and store it in a variable mtrxrows.
- Calculate the number of columns of the given matrix by calculating the length of the first list in the nested list using the len() function and store it in a variable mtrxcolums.
- Create a function to say checkdiagnolydominant_matx() which takes the given matrix and the number of rows of the given matrix as the arguments and returns true or false.
- Inside the function, Loop till the given number of rows using the For loop.
- Take a variable to say rslt_summ and initialize its value to 0.
-
Inside the For loop, Iterate till the given number of rows using another Nested For loop(Inner For loop).
- Add the absolute of mtrx[n][m] to the above-initialized rslt_summ and store it in the same variable.
- Remove the diagonal element by subtracting the abs(mtrx[n][n]) from the rslt_summ and store it in the same variable.
- Check if the abs(mtrx[n][n]) (diagonal element) is less than the rslt_summ(Which is the sum of non diagonal elements) using the if conditional statement.
- If it is true, then return False.
- Return True.
- Pass the given matrix and the number of rows of the given matrix as the arguments to the checkdiagnolydominant_matx() function and check if returns true or false using the if conditional statement.
- If it is true, print “Yes, the given matrix is a diagonally dominant matrix”.
- Else print “No, the given matrix is not a diagonally dominant matrix”.
- The Exit of the Program.
Below is the implementation:
# Create a function to say checkdiagnolydominant_matx() which takes the given matrix
# and the number of rows of the given matrix as the arguments and returns true or false
def checkdiagnolydominant_matx(mtrx, mtrxrows):
# Inside the function, Loop till the given number of rows using the For loop.
for n in range(0, mtrxrows):
# Take a variable to say rslt_summ and initialize its value to 0.
rslt_summ = 0
# Inside the For loop, Iterate till the given number of rows using another
# Nested For loop(Inner For loop).
for m in range(0, mtrxrows):
# Add the absolute of mtrx[n][m] to the above-initialized rslt_summ and store
# it in the same variable.
rslt_summ = rslt_summ + abs(mtrx[n][m])
# Remove the diagonal element by subtracting the abs(mtrx[n][n]) from the rslt_summ and
# store it in the same variable.
rslt_summ = rslt_summ - abs(mtrx[n][n])
# Check if the abs(mtrx[n][n]) (diagonal element) is less than the rslt_summ
# (Which is the #sum of non diagonal elements) using the if conditional statement.
if (abs(mtrx[n][n]) < rslt_summ):
# If it is true, then return False.
return False
# Return True.
return True
# Give the matrix as static input and store it in a variable.
mtrx = [[5, 1, 3], [2, 7, 1], [4, 0, 9]]
# Calculate the number of rows of the given matrix by
# calculating the length of the nested list using the len() function
# and store it in a variable mtrxrows.
mtrxrows = len(mtrx)
# Calculate the number of columns of the given matrix by
# calculating the length of the first list in the nested list
# using the len() function and store it in a variable mtrxcols.
mtrxcols = len(mtrx[0])
# Pass the given matrix and the number of rows of the given matrix as the arguments
# to the checkdiagnolydominant_matx() function and check if returns true or false
# using the if conditional statement.
if((checkdiagnolydominant_matx(mtrx, mtrxrows))):
# If it is true, print "Yes, the given matrix is a diagonally dominant matrix".
print("Yes, the given matrix is a diagonally dominant matrix")
else:
# Else print "No, the given matrix is not a diagonally dominant matrix".
print("No, the given matrix is not a diagonally dominant matrix")
Output:
Yes, the given matrix is a diagonally dominant matrix
Method #2: Using For loop (User Input)
Approach:
- Give the number of rows of the matrix as user input using the int(input()) function and store it in a variable.
- Give the number of columns of the matrix as user input using the int(input()) function and store it in another variable.
- Take a list and initialize it with an empty value using [] or list() to say gvnmatrix.
- Loop till the given number of rows using the For loop
- Inside the For loop, Give all the row elements of the given Matrix as a list using the list(),map(),int(),split() functions and store it in a variable.
- Add the above row elements list to gvnmatrix using the append() function.
- Create a function to say checkdiagnolydominant_matx() which takes the given matrix and the number of rows of the given matrix as the arguments and returns true or false.
- Inside the function, Loop till the given number of rows using the For loop.
- Take a variable to say rslt_summ and initialize its value to 0.
-
Inside the For loop, Iterate till the given number of rows using another Nested For loop(Inner For loop).
- Add the absolute of mtrx[n][m] to the above-initialized rslt_summ and store it in the same variable.
- Remove the diagonal element by subtracting the abs(mtrx[n][n]) from the rslt_summ and store it in the same variable.
- Check if the abs(mtrx[n][n]) (diagonal element) is less than the rslt_summ(Which is the sum of non diagonal elements) using the if conditional statement.
- If it is true, then return False.
- Return True.
- Pass the given matrix and the number of rows of the given matrix as the arguments to the checkdiagnolydominant_matx() function and check if returns true or false using the if conditional statement.
- If it is true, print “Yes, the given matrix is a diagonally dominant matrix”.
- Else print “No, the given matrix is not a diagonally dominant matrix”.
- The Exit of the Program.
Below is the implementation:
# Create a function to say checkdiagnolydominant_matx() which takes the given matrix
# and the number of rows of the given matrix as the arguments and returns true or false
def checkdiagnolydominant_matx(mtrx, mtrxrows):
# Inside the function, Loop till the given number of rows using the For loop.
for n in range(0, mtrxrows):
# Take a variable to say rslt_summ and initialize its value to 0.
rslt_summ = 0
# Inside the For loop, Iterate till the given number of rows using another
# Nested For loop(Inner For loop).
for m in range(0, mtrxrows):
# Add the absolute of mtrx[n][m] to the above-initialized rslt_summ and store
# it in the same variable.
rslt_summ = rslt_summ + abs(mtrx[n][m])
# Remove the diagonal element by subtracting the abs(mtrx[n][n]) from the rslt_summ and
# store it in the same variable.
rslt_summ = rslt_summ - abs(mtrx[n][n])
# Check if the abs(mtrx[n][n]) (diagonal element) is less than the rslt_summ
# (Which is the #sum of non diagonal elements) using the if conditional statement.
if (abs(mtrx[n][n]) < rslt_summ):
# If it is true, then return False.
return False
# Return True.
return True
# Give the number of rows of the matrix as user input using the int(input()) function
# and store it in a variable.
mtrxrows = int(input('Enter some random number of rows of the matrix = '))
# Give the number of columns of the matrix as user input using the int(input()) function
# and store it in another variable.
mtrxcols = int(input('Enter some random number of columns of the matrix = '))
# Take a list and initialize it with an empty value using [] or list() to say gvnmatrix.
mtrx = []
# Loop till the given number of rows using the For loop
for n in range(mtrxrows):
# Inside the For loop, Give all the row elements of the given Matrix as a list using
# the list(),map(),int(),split() functions and store it in a variable.
l = list(map(int, input(
'Enter {'+str(mtrxcols)+'} elements of row {'+str(n+1)+'} separated by spaces = ').split()))
# Add the above row elements list to gvnmatrix using the append() function.
mtrx.append(l)
if((checkdiagnolydominant_matx(mtrx, mtrxrows))):
# If it is true, print "Yes, the given matrix is a diagonally dominant matrix".
print("Yes, the given matrix is a diagonally dominant matrix")
else:
# Else print "No, the given matrix is not a diagonally dominant matrix".
print("No, the given matrix is not a diagonally dominant matrix")
Output:
Enter some random number of rows of the matrix = 3
Enter some random number of columns of the matrix = 3
Enter {3} elements of row {1} separated by spaces = 1 3 5
Enter {3} elements of row {2} separated by spaces = 2 4 6
Enter {3} elements of row {3} separated by spaces = 7 8 9
No, the given matrix is not a diagonally dominant matrix
The best way to learn Python for Beginners is to practice as much as they can taking help of the Sample Python Programs For Beginners. Using them you can develop code on your own and master coding skills.
