In the previous article, we have discussed Python Program to Find Slope of a Line
Given the base of the isosceles triangle, the task is to find the count of the maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle.
The side of the square must be parallel to the base of the given isosceles triangle.
Examples:
Example1:
Input:
Given base of triangle = 8
Output:
The maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle = 6
Explanation:
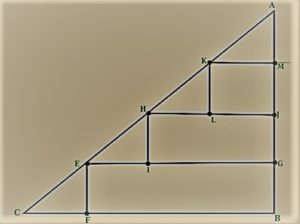
Example2:
Input:
Given base of triangle = 6
Output:
The maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle = 3
Program for Maximum Number of 2×2 Squares That Can be Fit Inside a Right Isosceles Triangle in python:
Below are the ways to find the count of the maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle:
Method #1: Using Mathematical Formula (Static Input)
Approach:
- Give the base of the triangle as static input and store it in a variable.
- Create a function to say count_Squares() which takes the given base of the isosceles triangle as an argument and returns the count of the maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle.
- Inside the function, subtract 2 from the given base value as it is the extra part.
- Store it in the same variable.
- Divide the given base of the triangle by 2 since each square has a base length of 2.
- Store it in the same variable.
- Calculate the value of gvn_trianglebase * (gvn_trianglebase + 1) / 2 (Mathematical Formula) and store it in another variable.
- Return the above result which is the count of the maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle.
- Pass the given base of the isosceles triangle to the count_Squares() function and print it.
- The Exit of the Program.
Below is the implementation:
# Create a function to say count_Squares() which takes the given base of the isosceles
# triangle as an argument and returns the count of the maximum number of 2*2
# squares required that can be fixed inside the given isosceles triangle.
def count_Squares(gvn_trianglebase):
# Inside the function, subtract 2 from the given base value as it is the extra part.
# Store it in the same variable.
gvn_trianglebase = (gvn_trianglebase - 2)
# Divide the given base of the triangle by 2 since each square has a base length of 2.
# Store it in the same variable.
gvn_trianglebase = gvn_trianglebase // 2
# Calculate the value of gvn_trianglebase * (gvn_trianglebase + 1) / 2
# (Mathematical Formula) and store it in another variable.
rslt = gvn_trianglebase * (gvn_trianglebase + 1) // 2
# Return the above result which is the count of the maximum number of 2*2 squares
# required that can be fixed inside the given isosceles triangle.
return rslt
# Give the base of the triangle as static input and store it in a variable.
gvn_trianglebase = 6
# Pass the given base of the isosceles triangle to the count_Squares() function
# and print it.
print("The maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle = ",
count_Squares(gvn_trianglebase))
Output:
The maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle = 3
Method #2: Using Mathematical Formula (User Input)
Approach:
- Give the base of the triangle as user input using the int(input()) function and store it in a variable.
- Create a function to say count_Squares() which takes the given base of the isosceles triangle as an argument and returns the count of the maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle.
- Inside the function, subtract 2 from the given base value as it is the extra part.
- Store it in the same variable.
- Divide the given base of the triangle by 2 since each square has a base length of 2.
- Store it in the same variable.
- Calculate the value of gvn_trianglebase * (gvn_trianglebase + 1) / 2 (Mathematical Formula) and store it in another variable.
- Return the above result which is the count of the maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle.
- Pass the given base of the isosceles triangle to the count_Squares() function and print it.
- The Exit of the Program.
Below is the implementation:
# Create a function to say count_Squares() which takes the given base of the isosceles
# triangle as an argument and returns the count of the maximum number of 2*2
# squares required that can be fixed inside the given isosceles triangle.
def count_Squares(gvn_trianglebase):
# Inside the function, subtract 2 from the given base value as it is the extra part.
# Store it in the same variable.
gvn_trianglebase = (gvn_trianglebase - 2)
# Divide the given base of the triangle by 2 since each square has a base length of 2.
# Store it in the same variable.
gvn_trianglebase = gvn_trianglebase // 2
# Calculate the value of gvn_trianglebase * (gvn_trianglebase + 1) / 2
# (Mathematical Formula) and store it in another variable.
rslt = gvn_trianglebase * (gvn_trianglebase + 1) // 2
# Return the above result which is the count of the maximum number of 2*2 squares
# required that can be fixed inside the given isosceles triangle.
return rslt
# Give the base of the triangle as user input using the int(input()) function
# and store it in a variable.
gvn_trianglebase = int(input("Enter some random number = "))
# Pass the given base of the isosceles triangle to the count_Squares() function
# and print it.
print("The maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle = ",
count_Squares(gvn_trianglebase))
Output:
Enter some random number = 8 The maximum number of 2*2 squares required that can be fixed inside the given isosceles triangle = 6
Find a comprehensive collection of Examples of Python Programs ranging from simple ones to complex ones to guide you throughout your coding journey.
