Hashing and Hash Table
- Hashing
- Hash Table
- Features of HashTable
- Adding element in HashTable
- Hashing Collisions
- Searching element in Hash Table
- Best Case Time Complexity in Hashing
- Worst Case Time Complexity in Hashing
1)Hashing
Hashing is the process of mapping object data to a representative integer value using a function or algorithm.
This hash code (or simply hash) can then be used to narrow our quest when searching for the item on the map.
These hash codes are usually used to create an index at which the value is stored.
2)Hash Table
A hash table is a data structure that stores data associatively. Data is stored in an array format in a hash table, with each data value having its own unique index value. When we know the index of the desired data, we can access it very quickly.
As a result, it becomes a data structure in which insertion and search operations are extremely quick, regardless of the size of the data. Hash Tables use an array as a storage medium and use the hash technique to produce an index from which an element is to be inserted or located.
3)Features of HashTable
- It works in the same way as HashMap, but it is synchronised.
- In a hash table, a key/value pair is stored.
- In Hashtable, we define an object that will be used as a key, as well as the value that will be associated with that key. The key is then hashed, and the resulting hash code serves as the index for storing the value in the table.
- The default capacity of the Hashtable class is 11, and the loadFactor is 0.75.
- HashMap does not support Enumeration, while Hashtable does not support fail-fast Enumeration.
4)Adding element in HashTable
When an entity is inserted into a Hash Table, its hash code is measured first, and the bucket in which it will be stored is determined based on that hash code.
Let us illustrate this with an example.
For instance, suppose we want to store some numbers in a Hash Table, i.e.
32 , 45 , 64 , 92 , 57 , 88 , 73
Internally, this Hash Table can use 10 buckets, i.e.
The Hash Code will be returned by our Hash Function.
HashCode=Element_value%10
This Hash code for,
32 will be 2
45 will be 5
64 will be 4
92 will be 2
57 will be 7
88 will be 8
73 will be 3
Now, each element’s hash code will be used to determine where that element will be stored, for example, 45 will be stored in bucket 5 since its hash code is 5. In the same way, all elements will be stored in the bucket that corresponds to their hash code.
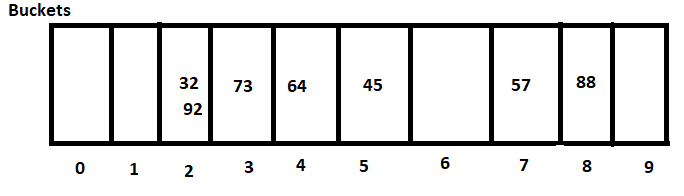
5)Hashing Collisions
As we can see, the hash code for both 32 and 92 is the same, which is 2. In Hashing, this is referred to as Collision. Both components would be deposited in the same bucket if they collide.
6)Searching element in Hash Table
If we want to check for an element in a hash table, we must first calculate the hash code for that element. Then, using the hash code, we’ll go straight to the bucket where this element will be saved. Now, there may be several elements in that bucket; in that case, we’ll look for our element only in those elements.
Assume we want to find 45 in the hash table in the previous case.
Then we’ll measure the hash code, which will be 45 %10 = 5.
Then we’ll go straight to bucket no. 5 and search for the factor there.
7)Best Case Time Complexity in Hashing
From the viewpoint of searching, each bucket containing only one element in the Hash table is the best case scenario. In such a case, searching time would require the following effort:
The complexity of calculating hash codes is O(1)
If the bucket only contains one element, choosing that element from the bucket is a complex task O(1)
Consequently In the best case scenario, finding an element would be difficult O(1)
While the complexity of a collision, i.e. several elements in a bucket, will be O(no. of elements in bucket), it will be much less than the complexity of searching an element from a List, which will be O(n).
8)Worst Case Time Complexity in Hashing
The worst case scenario in hashing is when the Hash Function is not correctly implemented, resulting in the same hash code for several elements.
Assume the following is our hash function:
Hash code = given_element / 100
Then, in the preceding case, the hash code for all elements ( 32 , 45 , 64 , 92 , 57 , 88 , 73 ) will be 0. As a result, all elements will be saved in bucket 0.
Since all components are in the same bucket, complexity is at its highest in this case. As a result, the complexity will be O(n) since it must check for the appropriate element among all elements.
Related Programs:
- what is the difference between final and immutable in java
- what is a dictionary in python and why do we need it
- what is an exception and how to do exception handling in java
- what is stddeque and how deque works internally
- what is a structured numpy array and how to create and sort it in python
- what is collection framework in java
- what is java 2 platform enterprise edition
