Python

In the previous article, we have discussed Python Program to Find the Center of the Circle using Endpoints of Diameter
When a chord is drawn in a circle, it divides the circle into two parts. These two parts of the circle are known as circle segments. The smaller area is referred to as the Minor segment, while the larger area is referred to as the Major segment.

Given the radius of the circle and the angle that forms a minor segment, the task is to find the areas of both major and minor segments of a circle.

Formula:

pi * r2 * (angle/360) – 1/2 * r2 * Sin(angle)

Examples:

Example1:

Input:

Given radius = 20
Given angle =  60 (degrees)

Output:

The minor segment area = 36.23434102950645
The major segment area = 1220.402189686826

Example2:

Input:

Given radius = 10.5
Given angle =  45

Output:

The minor segment area = 4.315801733342639
The major segment area = 342.0447026361856

Program to Find Area of a Circular Segment in Python

Below are the ways to find the areas of both major and minor segments of a circle in Python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Import math module using the import keyword.
• Give the radius as static input and store it in a variable.
• Give the angle as static input and store it in another variable.
• Take a variable and initialize the pi value as 3.14159.
• Create a function to say BothSegments_area() which takes the given radius and angle as the arguments, and returns the major and minor segments area.
• Inside the function, calculate the value area of the sector using the above given mathematical formula and store it in a variable.
• Calculate the area of the triangle using the above given mathematical formula and math.sin() function.
• Store it in another variable.
• Subtract the area of a triangle from the area of a sector and return it.
• Pass the given radius and angle as the arguments to the BothSegments_area() function and print the area of the minor segment.
• Pass the given radius and 360-angle as the arguments to the BothSegments_area() function and print the area of the major segment.
• The Exit of the Program.

Below is the implementation:

# Import math module using the import keyword.
import math

# Create a function to say BothSegments_area() which takes the given radius and angle
# as the arguments, and returns the major and minor segments area.


def BothSegments_area(gven_radius, gven_angl):
        # Inside the function, calculate the value area of the sector using the above
        # given mathematical formula and store it in a variable.
    rsltareaof_sectr = pi * (gven_radius * gven_radius) * (gven_angl / 360)

    # Calculate the area of the triangle using the above given mathematical formula and
    #  math.sin() function.
    # store it in another variable.
    rsltareaof_triangl = 1 / 2 * \
        (gven_radius * gven_radius) * math.sin((gven_angl * pi) / 180)

    # Subtract the area of a triangle from the area of a sector and return it.
    return rsltareaof_sectr - rsltareaof_triangl


# Give the radius as static input and store it in a variable.
gven_radius = 20
# Give the angle as static input and store it in another variable.
gven_angl = 60
# Take a variable and initialize the pi value as 3.14159.
pi = 3.14159
# Pass the given radius and angle as the arguments to the BothSegments_area()
# function and print the area of the minor segment.
print("The minor segment area =",
      BothSegments_area(gven_radius, gven_angl))
# Pass the given radius and 360-angle as the arguments to the BothSegments_area()
# function and print the area of the major segment.
print("The major segment area =",
      BothSegments_area(gven_radius, (360 - gven_angl)))

Output:

The minor segment area = 36.23434102950645
The major segment area = 1220.402189686826

Method #2: Using Mathematical Formula (User Input)

Approach:

• Import math module using the import keyword.
• Give the radius as user input using the float(input()) function and store it in a variable.
• Give the angle as user input using the float(input()) function and store it in another variable.
• Take a variable and initialize the pi value as 3.14159.
• Create a function to say BothSegments_area() which takes the given radius and angle as the arguments, and returns the major and minor segments area.
• Inside the function, calculate the value area of the sector using the above given mathematical formula and store it in a variable.
• Calculate the area of the triangle using the above given mathematical formula and math.sin() function.
• Store it in another variable.
• Subtract the area of a triangle from the area of a sector and return it.
• Pass the given radius and angle as the arguments to the BothSegments_area() function and print the area of the minor segment.
• Pass the given radius and 360-angle as the arguments to the BothSegments_area() function and print the area of the major segment.
• The Exit of the Program.

Below is the implementation:

# Import math module using the import keyword.
import math

# Create a function to say BothSegments_area() which takes the given radius and angle
# as the arguments, and returns the major and minor segments area.


def BothSegments_area(gven_radius, gven_angl):
        # Inside the function, calculate the value area of the sector using the above
        # given mathematical formula and store it in a variable.
    rsltareaof_sectr = pi * (gven_radius * gven_radius) * (gven_angl / 360)

    # Calculate the area of the triangle using the above given mathematical formula and
    #  math.sin() function.
    # store it in another variable.
    rsltareaof_triangl = 1 / 2 * \
        (gven_radius * gven_radius) * math.sin((gven_angl * pi) / 180)

    # Subtract the area of a triangle from the area of a sector and return it.
    return rsltareaof_sectr - rsltareaof_triangl


# Give the radius as user input using the float(input()) function and store it in a variable.
gven_radius = float(input("Enter some random number = "))
# Give the angle as as user input using the float(input()) function and
# store it in another variable.
gven_angl = float(input("Enter some random number = "))
# Take a variable and initialize the pi value as 3.14159.
pi = 3.14159
# Pass the given radius and angle as the arguments to the BothSegments_area()
# function and print the area of the minor segment.
print("The minor segment area =",
      BothSegments_area(gven_radius, gven_angl))
# Pass the given radius and 360-angle as the arguments to the BothSegments_area()
# function and print the area of the major segment.
print("The major segment area =",
      BothSegments_area(gven_radius, (360 - gven_angl)))

Output:

Enter some random number = 10.5
Enter some random number = 45
The minor segment area = 4.315801733342639
The major segment area = 342.0447026361856

If you wanna write simple python programs as a part of your coding practice refer to numerous Simple Python Program Examples existing and learn the approach used.

• Python Program to Check if a given Circle lies Completely Inside the Ring formed by Two Concentric Circles
• Python Program for Area of a Circumscribed Circle of a Square
• Python Program for Area of Square Circumscribed by Circle
• Python Program to Find the Center of the Circle using Endpoints of Diameter

In the previous article, we have discussed Python Program for Area of Square Circumscribed by Circle
Given two endpoints (x1, y1) and (x2, y2) of circles diameter, the task is to find the center of the circle for the given diameter endpoints in python.

Formula:

The center of the circle can be calculated by using the midpoint formula.

Midpoint(M) = ((x ₁ + x ₂) / 2, (y ₁ + y ₂) / 2)

Examples:

Example1:

Input:

Given First Point = ( 2, 4 ) 
Given Second Point = ( 6, -1)

Output:

The center of the circle for the given diameter endpoints is:
( 4 , 1 )

Example2:

Input:

Given First Point = ( 5, 2 )
Given Second Point = ( 1, 4 )

Output:

The center of the circle for the given diameter endpoints is:
( 3 , 3 )

Program to Find the Center of the Circle using Endpoints of Diameter in Python

Below are the ways to find the center of the circle for the given diameter endpoints in python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the first point as static input and store it in two variables.
• Give the second point as static input and store it in another two variables.
• Pass the given two endpoints of a diameter i.e, a1, a2, b1, b2 as the arguments to the FindCircle_Center() function.
• Create a function to say FindCircle_Center() which takes the given two endpoints of a diameter of circle i.e, a1, a2, b1, b2 as the arguments, and prints the center of the given circle.
• Calculate the x coordinate of the center of the given circle using the above given mathematical formula and store it in a variable.
• Calculate the y coordinate of the center of the given circle using the above given mathematical formula and store it in another variable.
• Print the center of the circle for the given diameter endpoints.
• The Exit of the Program.

Below is the implementation:

# Create a function to say FindCircle_Center() which takes the given two endpoints of
# a diameter of circle i.e, a1, a2, b1, b2 as the arguments, and prints the center
# of the given circle.


def FindCircle_Center(a1, a2, b1, b2):
    # Calculate the x coordinate of the center of the given circle using the above
    # given mathematical formula and store it in a variable.

    mid_x_Coordinate = int((a1 + a2) / 2)
    # Calculate the y coordinate of the center of the given circle using the above given
    # mathematical formula and store it in another variable.

    mid_y_Coordinate = int((b1 + b2) / 2)
    # Print the center of the circle for the given diameter endpoints.
    print("(", mid_x_Coordinate, ",", mid_y_Coordinate, ")")


# Give the first point as static input and store it in two variables.
a1 = 2
b1 = 4
# Give the second point as static input and store it in another two variables.
a2 = 6
b2 = -1
print("The center of the circle for the given diameter endpoints is:")
# Pass the given two endpoints of a diameter i.e, a1, a2, b1, b2 as the arguments to the
# FindCircle_Center() function.
FindCircle_Center(a1, a2, b1, b2)

Output:

The center of the circle for the given diameter endpoints is:
( 4 , 1 )

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the first point as user input using map(),int(),split() functions and store it in two variables.
• Give the second point as user input using map(),int(),split() functions and store it in two variables.
• Pass the given two endpoints of a diameter i.e, a1, a2, b1, b2 as the arguments to the FindCircle_Center() function.
• Create a function to say FindCircle_Center() which takes the given two endpoints of a diameter of circle i.e, a1, a2, b1, b2 as the arguments, and prints the center of the given circle.
• Calculate the x coordinate of the center of the given circle using the above given mathematical formula and store it in a variable.
• Calculate the y coordinate of the center of the given circle using the above given mathematical formula and store it in another variable.
• Print the center of the circle for the given diameter endpoints.
• The Exit of the Program.

Below is the implementation:

# Create a function to say FindCircle_Center() which takes the given two endpoints of
# a diameter of circle i.e, a1, a2, b1, b2 as the arguments, and prints the center
# of the given circle.


def FindCircle_Center(a1, a2, b1, b2):
    # Calculate the x coordinate of the center of the given circle using the above
    # given mathematical formula and store it in a variable.

    mid_x_Coordinate = int((a1 + a2) / 2)
    # Calculate the y coordinate of the center of the given circle using the above given
    # mathematical formula and store it in another variable.

    mid_y_Coordinate = int((b1 + b2) / 2)
    # Print the center of the circle for the given diameter endpoints.
    print("(", mid_x_Coordinate, ",", mid_y_Coordinate, ")")


# Give the first point as user input using map(),int(),split() functions
# and store it in two variables.
a1, b1 = map(int, input(
    'Enter some random first point values separated by spaces = ').split())
# Give the second point as user input using map(),int(),split() functions
# and store it in two variables.
a2, b2 = map(int, input(
    'Enter some random second point values separated by spaces = ').split())
print("The center of the circle for the given diameter endpoints is:")
# Pass the given two endpoints of a diameter i.e, a1, a2, b1, b2 as the arguments to the
# FindCircle_Center() function.
FindCircle_Center(a1, a2, b1, b2)

Output:

Enter some random first point values separated by spaces = 5 2
Enter some random second point values separated by spaces = 1 4
The center of the circle for the given diameter endpoints is:
( 3 , 3 )

Find a comprehensive collection of Examples of Python Programs ranging from simple ones to complex ones to guide you throughout your coding journey.

• Python Program to Check If a Line Touches or Intersects a Circle
• Python Program to Check if a given Circle lies Completely Inside the Ring formed by Two Concentric Circles
• Python Program for Area of a Circumscribed Circle of a Square
• Python Program for Area of Square Circumscribed by Circle

In the previous article, we have discussed Python Program for Area of a Circumscribed Circle of a Square
Given the radius of the circle, the task is to calculate the area of a square circumscribed by the circle.

Formula:

The formula to find the area of a square circumscribed by the circle = 2*(radius**2)

Where ** indicates power value

Examples:

Example1:

Input:

Given radius = 8

Output:

The area of a square circumscribed by the circle for the given radius{ 8 } =  128

Example2:

Input:

Given radius = 5

Output:

The area of a square circumscribed by the circle for the given radius{ 5 } =  50

Program for Area of Square Circumscribed by Circle in Python

Below are the ways to calculate the area of a square circumscribed by the circle in Python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the radius as static input and store it in a variable.
• Create a function to say Areacircumscribd_square() which takes the given radius of the circle as an argument, and returns the area of a square circumscribed by the circle.
• Inside the function, calculate the area of a square circumscribed by the circle using the above mathematical formula and store it in a variable.
• Return the above result.
• Pass the given radius as an argument to the Areacircumscribd_square() function and store it in another variable.
• Print the above result by rounding off to the 2 places after the decimal point using the round() function.
• The Exit of the Program.

Below is the implementation:

# Create a function to say Areacircumscribd_square() which takes the given radius of
# the circle as an argument, and returns the area of a square circumscribed
# by the circle.


def Areacircumscribd_square(gvn_radiuss):
    # Inside the function, calculate the area of a square circumscribed by the circle
    # using the above mathematical formula and store it in a variable.
    area_squar = (2 * gvn_radiuss * gvn_radiuss)
    # Return the above result.
    return area_squar


# Give the radius as static input and store it in a variable.
gvn_radiuss = 8
# Pass the given radius as an argument to the Areacircumscribd_square() function and
# store it in another variable.
fnl_rsltarea = Areacircumscribd_square(gvn_radiuss)
# Print the above result by rounding off to the 2 places after the decimal point
# using the round() function.
print("The area of a square circumscribed by the circle for the given radius{", gvn_radiuss, "} = ", round(
    fnl_rsltarea, 2))

Output:

The area of a square circumscribed by the circle for the given radius{ 8 } =  128

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the radius as user input using the float(input()) function and store it in a variable.
• Create a function to say Areacircumscribd_square() which takes the given radius of the circle as an argument, and returns the area of a square circumscribed by the circle.
• Inside the function, calculate the area of a square circumscribed by the circle using the above mathematical formula and store it in a variable.
• Return the above result.
• Pass the given radius as an argument to the Areacircumscribd_square() function and store it in another variable.
• Print the above result by rounding off to the 2 places after the decimal point using the round() function.
• The Exit of the Program.

Below is the implementation:

# Create a function to say Areacircumscribd_square() which takes the given radius of
# the circle as an argument, and returns the area of a square circumscribed
# by the circle.


def Areacircumscribd_square(gvn_radiuss):
    # Inside the function, calculate the area of a square circumscribed by the circle
    # using the above mathematical formula and store it in a variable.
    area_squar = (2 * gvn_radiuss * gvn_radiuss)
    # Return the above result.
    return area_squar


# Give the radius as user input using the float(input()) function and store it in a variable.
gvn_radiuss = float(input("Enter some random number = "))
# Pass the given radius as an argument to the Areacircumscribd_square() function and
# store it in another variable.
fnl_rsltarea = Areacircumscribd_square(gvn_radiuss)
# Print the above result by rounding off to the 2 places after the decimal point
# using the round() function.
print("The area of a square circumscribed by the circle for the given radius{", gvn_radiuss, "} = ", round(
    fnl_rsltarea, 2))

Output:

Enter some random number = 5
The area of a square circumscribed by the circle for the given radius{ 5.0 } = 50.0

Find the best practical and ready-to-use Python Programming Examples that you can simply run on a variety of platforms and never stop learning.

• Python Program for Pizza Cut Problem (Or Circle Division by Lines)
• Python Program to Check If a Line Touches or Intersects a Circle
• Python Program to Check if a given Circle lies Completely Inside the Ring formed by Two Concentric Circles
• Python Program for Area of a Circumscribed Circle of a Square

In the previous article, we have discussed Python Program to Check if a given Circle lies Completely Inside the Ring formed by Two Concentric Circles
Given the side length of a square, the task is to calculate the area of a circumscribed circle around the given square.

Formula:

(pi * s* s)/2

where pi= 3.14159265

s = side length of square.

Examples:

Example1:

Input:

Given side of square = 5

Output:

The area of an circumscribed circle is for a given square of side { 5 } =  39.27

Example2:

Input:

Given side of square = 8

Output:

The area of an circumscribed circle is for a given square of side { 8 } =  100.53

Program for Area of a Circumscribed Circle of a Square in Python

Below are the ways to calculate the area of a circumscribed circle around the given square in python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the side of a square as static input and store it in a variable.
• Take a variable and initialize it with the pi value of 3.14159265.
• Create a function to say Find_areacircumscribdcirle() which takes the given side length of the square as an argument, and returns the area of a circumscribed circle around the given square.
• Inside the function, calculate the area of a circumscribed circle around the given square using the above mathematical formula and store it in a variable.
• Return the above result.
• Pass the given side length of the square as an argument to the Find_areacircumscribdcirle() function and store it in another variable.
• Print the above result by rounding off to the 2 places after the decimal point using the round() function.
• The Exit of the Program.

Below is the implementation:

# Create a function to say Find_areacircumscribdcirle() which takes the given side
# length of the square as an argument, and returns the area of a circumscribed
# circle around the given square.


def Find_areacircumscribdcirle(sideof_sqre):
    # Inside the function, calculate the area of a circumscribed circle around the given
    # square using the above mathematical formula and store it in a variable.
    circl_area = (sideof_sqre * sideof_sqre * (pi / 2))
    # Return the above result.
    return circl_area


# Give the side of a square as static input and store it in a variable.
sideof_sqre = 5
# Take a variable and initialize it with the pi value of 3.14159265.
pi = 3.14159265
# Pass the given side length of the square as an argument to the
# Find_areacircumscribdcirle() function and store it in another variable.
fnl_rsltarea = Find_areacircumscribdcirle(sideof_sqre)
# Print the above result by rounding off to the 2 places after the decimal point using
# the round() function.
print("The area of an circumscribed circle is for a given square of side {", sideof_sqre, "} = ",
      round(fnl_rsltarea, 2))

Output:

The area of an circumscribed circle is for a given square of side { 5 } =  39.27

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the side of a square as user input using the float(input()) function and store it in a variable.
• Take a variable and initialize it with the pi value of 3.14159265.
• Create a function to say Find_areacircumscribdcirle() which takes the given side length of the square as an argument, and returns the area of a circumscribed circle around the given square.
• Inside the function, calculate the area of a circumscribed circle around the given square using the above mathematical formula and store it in a variable.
• Return the above result.
• Pass the given side length of the square as an argument to the Find_areacircumscribdcirle() function and store it in another variable.
• Print the above result by rounding off to the 2 places after the decimal point using the round() function.
• The Exit of the Program.

Below is the implementation:

# Create a function to say Find_areacircumscribdcirle() which takes the given side
# length of the square as an argument, and returns the area of a circumscribed
# circle around the given square.


def Find_areacircumscribdcirle(sideof_sqre):
    # Inside the function, calculate the area of a circumscribed circle around the given
    # square using the above mathematical formula and store it in a variable.
    circl_area = (sideof_sqre * sideof_sqre * (pi / 2))
    # Return the above result.
    return circl_area


# Give the side of a square as user input using the float(input()) function and
# store it in a variable.
sideof_sqre = float(input("Enter some random number = "))
# Take a variable and initialize it with the pi value of 3.14159265.
pi = 3.14159265
# Pass the given side length of the square as an argument to the
# Find_areacircumscribdcirle() function and store it in another variable.
fnl_rsltarea = Find_areacircumscribdcirle(sideof_sqre)
# Print the above result by rounding off to the 2 places after the decimal point using
# the round() function.
print("The area of an circumscribed circle is for a given square of side {", sideof_sqre, "} = ",
      round(fnl_rsltarea, 2))

Output:

Enter some random number = 8
The area of an circumscribed circle is for a given square of side { 8.0 } = 100.53

Access the big list of Python Programming Code Examples with actual logical code asked in Programming and Coding Interviews for Python and stand out from the crowd.

• Python Program to Check Whether Triangle is Valid or Not if Sides are Given
• Python Program for Pizza Cut Problem (Or Circle Division by Lines)
• Python Program to Check If a Line Touches or Intersects a Circle
• Python Program to Check if a given Circle lies Completely Inside the Ring formed by Two Concentric Circles

In the previous article, we have discussed Python Program to Check If a Line Touches or Intersects a Circle
Given two circles of radius r and R, their centers are both at the origin. Given another circle with radius r1 and center at (x1, y1). Check to see if the third circle (circle of radius r1) is entirely contained within the ring formed by two circles of radius r and R

Examples:

Example1:

Input:

Given r = 8
Given R = 4
Given r1 = 2
Given x1 = 6
Given y1 = 0

Output:

The given circle lies inside the ring

Example2:

Input:

Given r = 7
Given R = 10
Given r1 = 5
Given x1 = 2
Given y1 = 6

Output:

The given circle does not lies inside the ring

Program to Check if a given Circle lies Completely Inside the Ring formed by Two Concentric Circles

Below are the ways to check if the given circle is enclosed completely inside the ring formed by the given two circles in Python:

• Using Mathematical Approach (Static Input)
• Using Mathematical Approach (User Input)

Pythagoras’ Theorem can be used to solve this problem. Using Pythagoras’ theorem, calculate the distance between the center of the circle and the origin, denoted by ‘dis’.
Simply check that the value of (dis – r1)> = r and (dis + r1)< = R after computing the distance. If both of these conditions are met, the circle is completely enclosed within the ring.

Method #1: Using Mathematical Approach(Static Input)

Approach:

• import the math module using the import keyword
• Give the first circle radius(small circle) r as static input and store it in a variable say rVal.
• Give the second circle radius (Big circle) R as static input and store it in another variable say RVal.
• Give the Third Circle(Which we want to check Condition) radius r1 as static input and store it in another variable say r1Val.
• Give the x coordinates and y coordinates of the third circle and store them in two separate variables.
• Calculate the distance(dis value) using Pythagoras theorem and sqrt() function and store the result in a variable say disVal.
• Check the Condition (dis – r1)> = r and (dis + r1)< = R using the if conditional Statement.
• If it is true then Print the given circle inside the ring
• Else print the circle does not lie inside.
• The Exit of the Program.

Below is the implementation:

# import the math module using the import keyword
import math
# Give the first circle radius(small circle) r as static input and
# store it in a variable say rVal.
rVal = 8
# Give the second circle radius (Big circle) R as static input and
# store it in another variable say RVal.
RVal = 4
# Give the Third Circle(Which we want to check Condition) radius r1 as
# static input and store it in another variable say r1Val
r1Val = 2
# Give the x coordinates and y coordinates of the third circle and
# store them in two separate variables.
xCoordinate = 6
yCoordinate = 0
# Calculate the distance(dis value) using Pythagoras theorem and sqrt() function
# and store the result in a variable say disVal.
disVal = math.sqrt(xCoordinate * xCoordinate + yCoordinate * yCoordinate)
# Check the Condition (dis – r1)> = r and (dis + r1)< = R 
# using the if conditional Statement.
if((disVal-r1Val >= RVal and disVal+r1Val <= rVal)):
    # If it is true then Print the given circle inside the ring 
    print('The given circle lies inside the ring')
else:
    # Else print the circle does not lie inside.
    print('The given circle does not lies inside the ring')

Output:

The given circle lies inside the ring

Method #2: Using Mathematical Approach (User Input)

Approach:

• import the math module using the import keyword
• Give the first circle radius(small circle) r as user input using the int(input()) function and store it in a variable say rVal.
• Give the second circle radius (Big circle) R as user input using the int(input()) function and store it in another variable say RVal.
• Give the Third Circle(Which we want to check Condition) radius r1 as user input using the int(input()) function and store it in another variable say r1Val.
• Give the x coordinates and y coordinates of the third circle as user input using the map, input(), int(), split() function and store them in two separate variables.
• Calculate the distance(dis value) using Pythagoras theorem and sqrt() function and store the result in a variable say disVal.
• Check the Condition (dis – r1)> = r and (dis + r1)< = R using the if conditional Statement.
• If it is true then Print the given circle inside the ring
• Else print the circle does not lie inside.
• The Exit of the Program.

Below is the implementation:

# import the math module using the import keyword
import math
# Give the first circle radius(small circle) r as user input using the int(input()) function and store it in a variable say rVal.
rVal = int(input('Enter some random first circle radius = '))
# Give the second circle radius (Big circle) R as user input using the int(input()) function and store it in another variable say RVal.
RVal = int(input('Enter some random second circle radius = '))
# Give the Third Circle(Which we want to check Condition) radius r1 as user input using the int(input()) function and store it in another variable say r1Val.
r1Val = int(input('Enter some random Third circle radius = '))
# Give the x coordinates and y coordinates of the third circle as user input using the map, input(), int(), split() function
# and store them in two separate variables.
xCoordinate, yCoordinate = map(int, input(
    'Enter some random x and y coordinates separated by spaces = ').split())
# Calculate the distance(dis value) using Pythagoras theorem and sqrt() function
# and store the result in a variable say disVal.
disVal = math.sqrt(xCoordinate * xCoordinate + yCoordinate * yCoordinate)
# Check the Condition (dis – r1)> = r and (dis + r1)< = R 
# using the if conditional Statement.
if((disVal-r1Val >= RVal and disVal+r1Val <= rVal)):
    # If it is true then Print the given circle inside the ring 
    print('The given circle lies inside the ring')
else:
    # Else print the circle does not lie inside.
    print('The given circle does not lies inside the ring')

Output:

Enter some random first circle radius = 7
Enter some random second circle radius = 10
Enter some random Third circle radius = 5
Enter some random x and y coordinates separated by spaces = 2 6
The given circle does not lies inside the ring

The best way to learn Python for Beginners is to practice as much as they can taking help of the Sample Python Programs For Beginners. Using them you can develop code on your own and master coding skills.

• Python Program for Triangular Matchstick Number
• Python Program to Check Whether Triangle is Valid or Not if Sides are Given
• Python Program for Pizza Cut Problem (Or Circle Division by Lines)
• Python Program to Check If a Line Touches or Intersects a Circle

In the previous article, we have discussed Python Program for Pizza Cut Problem (Or Circle Division by Lines)
Given the coordinates of the center point as (0,0), the radius of the circle, and the equation of a line and the task is to check whether the given line touches or intersects the circle.

The line equation is in the form ax+by+c.

Hence a, b, c values are given for a line equation.

The three possibilities :

• The Line intersect the circle
• The Line touches the circle
• The Line outside the circle

The following formula can be used to calculate the distance of a line from a point:

(ax+by+c)/sqrt(a*a+b*b)

If d > r,  the line lies outside the circle.
If d = r,  the line touches the circle.
If d < r,  the line intersects the circle.

where d = the distance of a line from a center.

r is the radius of the circle.

Examples:

Example1:

Input:

Given radius = 6
Given  a = 2
Given  b = 1
Given  c = 1

Output:

The Given line intersects the circle

Example2:

Input:

Given radius = 5
Given a = 1
Given b = 1
Given c = -15

Output:

The Given line is outside the circle

Program to Check If a Line Touches or Intersects a Circle in Python

Below are the ways to check whether the given line touches or intersects the circle in Python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Import math module using the import keyword.
• Give the radius as static input and store it in a variable.
• Take the x-coordinate of the center and initialize its value to 0.
• Take the y-coordinate of the center and initialize its value to 0.
• Give the number as static input and store it in a variable.
• Give the other number as static input and store it in another variable.
• Give the third number as static input and store it in another variable.
• Calculate the distance of the given line from the given center point using the above given mathematical formula, abs(), math.sqrt() functions.
• Store it in another variable.
• Check if the given radius value is equal to the above-obtained distance using the if conditional statement.
• If it is true, then print “The Given line touches the circle”.
• Check if the given radius value is greater than the above-obtained distance using the elif conditional statement.
• If it is true, then print “The Given line intersects the circle”.
• Else, print “The Given line is outside the circle”.
• The Exit of the Program.

Below is the implementation:

# Import math module using the import keyword.
import math
# Give the radius as static input and store it in a variable.
gvn_radiuss = 6
# Take the x-coordinate of center and initialize its value to 0.
m = 0
# Take the y-coordinate of center and initialize its value to 0.
n = 0
# Give the number as static input and store it in a variable.
p = 2
# Give the other number as static input and store it in another variable.
q = 1
# Give the third number as static input and store it in another variable.
r = 1
# Calculate the distance of the given line from the given center point using the
# above given mathematical formula, abs(), math.sqrt() functions
# store it in another variable.
distancee_val = ((abs(p * m + q * n + r)) /
                 math.sqrt(p * p + q * q))
# Check if the given radius value is equal to the above obtained distance using the
# if conditional statement.
if (gvn_radiuss == distancee_val):
    # If it is true, then print "The Given line touches the circle".
    print("The Given line touches the circle")
# Check if the given radius value is greater than the above obtained distance using
# the elif conditional statement.
elif (gvn_radiuss > distancee_val):
    # If it is true, then print "The Given line intersects the circle".
    print("The Given line intersects the circle")
else:
    # Else, print "The Given line is outside the circle".
    print("The Given line is outside the circle")

Output:

The Given line intersects the circle

Method #2: Using Mathematical Formula (User Input)

Approach:

• Import math module using the import keyword.
• Give the radius as user input using the int(input()) function and store it in a variable.
• Take the x-coordinate of the center and initialize its value to 0.
• Take the y-coordinate of the center and initialize its value to 0.
• Give the number as user input using the int(input()) function and store it in a variable.
• Give the other number as user input using the int(input()) function and store it in another variable.
• Give the third number as user input using the int(input()) function and store it in another variable.
• Calculate the distance of the given line from the given center point using the above given mathematical formula, abs(), math.sqrt() functions.
• Store it in another variable.
• Check if the given radius value is equal to the above-obtained distance using the if conditional statement.
• If it is true, then print “The Given line touches the circle”.
• Check if the given radius value is greater than the above-obtained distance using the elif conditional statement.
• If it is true, then print “The Given line intersects the circle”.
• Else, print “The Given line is outside the circle”.
• The Exit of the Program.

Below is the implementation:

# Import math module using the import keyword.
import math
# Give the radius as user input using the int(input()) function and 
# store it in a variable.
gvn_radiuss = int(input("Enter some random number = "))
# Take the x-coordinate of center and initialize its value to 0.
m = 0
# Take the y-coordinate of center and initialize its value to 0.
n = 0
# Give the number as user input using the int(input()) function and store it in a variable.
p = int(input("Enter some random number = "))
# Give the other number as user input using the int(input()) function and store it in another variable.
q = int(input("Enter some random number = "))
# Give the third number as user input using the int(input()) function and store it in another variable.
r = int(input("Enter some random number = "))
# Calculate the distance of the given line from the given center point using the
# above given mathematical formula, abs(), math.sqrt() functions
# store it in another variable.
distancee_val = ((abs(p * m + q * n + r)) /
                 math.sqrt(p * p + q * q))
# Check if the given radius value is equal to the above obtained distance using the
# if conditional statement.
if (gvn_radiuss == distancee_val):
    # If it is true, then print "The Given line touches the circle".
    print("The Given line touches the circle")
# Check if the given radius value is greater than the above obtained distance using
# the elif conditional statement.
elif (gvn_radiuss > distancee_val):
    # If it is true, then print "The Given line intersects the circle".
    print("The Given line intersects the circle")
else:
    # Else, print "The Given line is outside the circle".
    print("The Given line is outside the circle")

Output:

Enter some random number = 5
Enter some random number = 1
Enter some random number = 1
Enter some random number = -15
The Given line is outside the circle

Enhance your coding skills with our list of Python Basic Programs provided and become a pro in the general-purpose programming language Python in no time.

• Python Program for Maximum Number of Squares that Can Fit in a Right Angle Isosceles Triangle
• Python Program for Triangular Matchstick Number
• Python Program to Check Whether Triangle is Valid or Not if Sides are Given
• Python Program for Pizza Cut Problem (Or Circle Division by Lines)

In the previous article, we have discussed Python Program to Check Whether Triangle is Valid or Not if Sides are Given
Given the number of cuts and the task is to get the maximum number of pieces from the given number of cuts in python.

Formula:

1 + n*(n+1)/2

where n= number of cuts.

Examples:

Example1:

Input:

Given number of cuts = 4

Output:

The maximum number of pieces from the given number of cuts =  11

Example2:

Input:

Given number of cuts = 5

Output:

The maximum number of pieces from the given number of cuts =  16

Program for Pizza Cut Problem (Or Circle Division by Lines) in Python

Below are the ways to get the maximum number of pieces from the given number of cuts in python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the number of cuts as static input and store it in a variable.
• Create a function to say Get_Max_Pieces() which takes the given number of cuts as an argument, and returns the maximum number of pieces from the given number of cuts.
• Inside the function, calculate the maximum number of pieces by using the above given mathematical formula and convert it to an integer using the int() function.
• Store it in another variable.
• Return the above result.
• Pass the given number of cuts as an argument to the Get_Max_Pieces() function and store it in another variable.
• Print the above result which is the maximum number of pieces from the given number of cuts.
• The Exit of the Program.

Below is the implementation:

# Create a function to say Get_Max_Pieces() which takes the given number of cuts as
# an argument, and returns the maximum number of pieces from the given number of cuts.


def Get_Max_Pieces(no_of_cuts):
    # Inside the function, calculate the maximum number of pieces by using the above
        # given mathematical formula and convert it to an integer using the int() function.
        # Store it in another variable.
    k = int(1 + no_of_cuts * (no_of_cuts + 1) / 2)
    # Return the above result.
    return k


# Give the number of cuts as static input and store it in a variable.
no_of_cuts = 4
# Pass the given number of cuts as an argument to the Get_Max_Pieces() function
# and store it in another variable.
maxim_pieces = Get_Max_Pieces(no_of_cuts)
# Print the above result which is the maximum number of pieces from the given
# number of cuts.
print("The maximum number of pieces from the given number of cuts = ", maxim_pieces)

Output:

The maximum number of pieces from the given number of cuts =  11

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the number of cuts as user input using the int(input()) function and store it in a variable.
• Create a function to say Get_Max_Pieces() which takes the given number of cuts as an argument, and returns the maximum number of pieces from the given number of cuts.
• Inside the function, calculate the maximum number of pieces by using the above given mathematical formula and convert it to an integer using the int() function.
• Store it in another variable.
• Return the above result.
• Pass the given number of cuts as an argument to the Get_Max_Pieces() function and store it in another variable.
• Print the above result which is the maximum number of pieces from the given number of cuts.
• The Exit of the Program.

Below is the implementation:

# Create a function to say Get_Max_Pieces() which takes the given number of cuts as
# an argument, and returns the maximum number of pieces from the given number of cuts.


def Get_Max_Pieces(no_of_cuts):
    # Inside the function, calculate the maximum number of pieces by using the above
        # given mathematical formula and convert it to an integer using the int() function.
        # Store it in another variable.
    k = int(1 + no_of_cuts * (no_of_cuts + 1) / 2)
    # Return the above result.
    return k


# Give the number of cuts as user input using the int(input()) function 
# and store it in a variable.
no_of_cuts = int(input("Enter some random number = "))
# Pass the given number of cuts as an argument to the Get_Max_Pieces() function
# and store it in another variable.
maxim_pieces = Get_Max_Pieces(no_of_cuts)
# Print the above result which is the maximum number of pieces from the given
# number of cuts.
print("The maximum number of pieces from the given number of cuts = ", maxim_pieces)

Output:

Enter some random number = 5
The maximum number of pieces from the given number of cuts = 16

Dive into numerous Python Programming Language Examples for practice and get the best out of the tutorial and learn python one step at a time.

• Python Program for Minimum Height of a Triangle with Given Base and Area
• Python Program for Maximum Number of Squares that Can Fit in a Right Angle Isosceles Triangle
• Python Program for Triangular Matchstick Number
• Python Program to Check Whether Triangle is Valid or Not if Sides are Given

In the previous article, we have discussed Python Program for Triangular Matchstick Number
Given three sides of a triangle, the task is to check if the given triangle is valid or not for the given 3 sides in python.

A triangle is said to be valid if the sum of its two sides is greater than the third side.

Conditions to check if the given triangle is valid or Not:

Let a, b, c  are the 3 sides of a triangle. It must satisfy the following conditions:

a + b > c

a + c > b

b + c > a

Example1:

Input:

Given First side = 5
Given Second side = 7
Given Third side = 6

Output:

Yes, the triangle is valid for the given three sides

Example2:

Input:

Given First side = 4
Given Second side = 9
Given Third side = 2

Output:

The triangle is invalid for the given three sides

Program to Check Whether Triangle is Valid or Not if Sides are Given in Python

Below are the ways to check if the given triangle is valid or not for the given 3 sides in python:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the first side of a triangle as static input and store it in a variable.
• Give the second side as static input and store it in another variable.
• Give the third side as static input and store it in another variable.
• Check if (fst_side + scnd_side <= thrd_side) or (fst_side + thrd_side <= scnd_side) or (scnd_side + thrd_side <= fst_side) using the if conditional statement.
• If it is true, then print “The triangle is invalid for the given three sides”.
• Else print “Yes, the triangle is valid for the given three sides”.
• The Exit of the Program.

Below is the implementation:

# Give the first side of a triangle as static input and store it in a variable.
fst_side = 5
# Give the second side as static input and store it in another variable.
scnd_side = 7
# Give the third side as static input and store it in another variable.
thrd_side = 6
# Check if (fst_side + scnd_side <= thrd_side) or (fst_side + thrd_side <= scnd_side)
# or (scnd_side + thrd_side <= fst_side) using the if conditional statement.
if (fst_side + scnd_side <= thrd_side) or (fst_side + thrd_side <= scnd_side) or (scnd_side + thrd_side <= fst_side):
    # If it is true, then print "The triangle is invalid for the given three sides".
    print("The triangle is invalid for the given three sides")
else:
    # Else print "Yes, the triangle is valid for the given three sides"
    print("Yes, the triangle is valid for the given three sides")

Output:

Yes, the triangle is valid for the given three sides

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the first side of a triangle as user input using the int(input()) function and store it in a variable.
• Give the second side as user input using the int(input()) function and store it in another variable.
• Give the third side as user input using the int(input()) function and store it in another variable.
• Check if (fst_side + scnd_side <= thrd_side) or (fst_side + thrd_side <= scnd_side) or (scnd_side + thrd_side <= fst_side) using the if conditional statement.
• If it is true, then print “The triangle is invalid for the given three sides”.
• Else print “Yes, the triangle is valid for the given three sides”.
• The Exit of the Program.

Below is the implementation:

# Give the first side of a triangle as user input using the int(input()) function and
# store it in a variable.
fst_side = int(input("Enter some random number = "))
# Give the second side as user input using the int(input()) function and
# store it in another variable.
scnd_side = int(input("Enter some random number = "))
# Give the third side as user input using the int(input()) function and
# store it in another variable.
thrd_side = int(input("Enter some random number = "))
# Check if (fst_side + scnd_side <= thrd_side) or (fst_side + thrd_side <= scnd_side)
# or (scnd_side + thrd_side <= fst_side) using the if conditional statement.
if (fst_side + scnd_side <= thrd_side) or (fst_side + thrd_side <= scnd_side) or (scnd_side + thrd_side <= fst_side):
    # If it is true, then print "The triangle is invalid for the given three sides".
    print("The triangle is invalid for the given three sides")
else:
    # Else print "Yes, the triangle is valid for the given three sides"
    print("Yes, the triangle is valid for the given three sides")

Output:

Enter some random number = 4
Enter some random number = 9
Enter some random number = 2
The triangle is invalid for the given three sides

If you are new to the Python Programming Language then practice using our Python Programming Examples for Beginners as our expert team has designed them from scratch.

• Python Program to Calculate Volume and Surface Area of Hemisphere
• Python Program for Minimum Height of a Triangle with Given Base and Area
• Python Program for Maximum Number of Squares that Can Fit in a Right Angle Isosceles Triangle
• Python Program for Triangular Matchstick Number

In the previous article, we have discussed Python Program for Maximum Number of Squares that Can Fit in a Right Angle Isosceles Triangle
Given a number x, which is the floor of the matchstick pyramid and the task is to find the number of matchsticks needed to form a pyramid of matchsticks of x floors.

Formula:

(3*x*(x+1))/2

Examples:

Example1:

Input:

Given number of floors = 3

Output:

The Number of matchsticks needed to form a pyramid of matchsticks :
18

Example2:

Input:

Given number of floors = 5

Output:

The Number of matchsticks needed to form a pyramid of matchsticks :
45

Program for Triangular Matchstick Number in Python

Below are the ways to find the number of matchsticks needed to form a pyramid of matchsticks of x floors:

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the number as static input and store it in a variable.
• Create a function to say count_MatchSticks() which takes the given number as an argument and returns the count of the number of matchsticks needed to form a pyramid of matchsticks for a given number of floors.
• Inside the function, calculate the number of matchsticks needed using the above given mathematical formula and store it in a variable.
• Return the above result.
• Pass the given number as an argument to the count_MatchSticks() function, convert it into an integer using the int() function and print it.
• The Exit of the Program.

Below is the implementation:

# Create a function to say count_MatchSticks() which takes the given number as an
# argument and returns the count of the number of matchsticks needed to form a
# pyramid of matchsticks for a given number of floors.


def count_MatchSticks(no_floors):
    # Inside the function, calculate the number of matchsticks needed using the above
    # given mathematical formula and store it in a variable.
    no_sticks = (3 * no_floors * (no_floors + 1)) / 2
    # Return the above result.
    return no_sticks


# Give the number as static input and store it in a variable.
no_floors = 3
print("The Number of matchsticks needed to form a pyramid of matchsticks :")
# Pass the given number as an argument to the count_MatchSticks() function, convert
# it into an integer using the int() function and print it.
print(int(count_MatchSticks(no_floors)))

Output:

The Number of matchsticks needed to form a pyramid of matchsticks :
18

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the number as user input using the int(input()) function and store it in a variable.
• Create a function to say count_MatchSticks() which takes the given number as an argument and returns the count of the number of matchsticks needed to form a pyramid of matchsticks for a given number of floors.
• Inside the function, calculate the number of matchsticks needed using the above given mathematical formula and store it in a variable.
• Return the above result.
• Pass the given number as an argument to the count_MatchSticks() function, convert it into an integer using the int() function and print it.
• The Exit of the Program.

Below is the implementation:

# Create a function to say count_MatchSticks() which takes the given number as an
# argument and returns the count of the number of matchsticks needed to form a
# pyramid of matchsticks for a given number of floors.


def count_MatchSticks(no_floors):
    # Inside the function, calculate the number of matchsticks needed using the above
    # given mathematical formula and store it in a variable.
    no_sticks = (3 * no_floors * (no_floors + 1)) / 2
    # Return the above result.
    return no_sticks


# Give the number as user input using the int(input()) function and store it in a variable.
no_floors = int(input("Enter some random number = "))
print("The Number of matchsticks needed to form a pyramid of matchsticks :")
# Pass the given number as an argument to the count_MatchSticks() function, convert
# it into an integer using the int() function and print it.
print(int(count_MatchSticks(no_floors)))

Output:

Enter some random number = 5
The Number of matchsticks needed to form a pyramid of matchsticks :
45

Remediate your knowledge gap by attempting the Python Code Examples regularly and understand the areas of need and work on them.

• Python Program to Calculate Volume of Dodecahedron
• Python Program to Calculate Volume and Surface Area of Hemisphere
• Python Program for Minimum Height of a Triangle with Given Base and Area
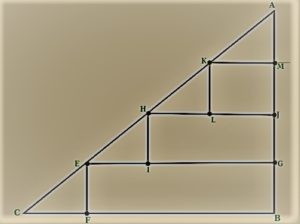
• Python Program for Maximum Number of Squares that Can Fit in a Right Angle Isosceles Triangle

In the previous article, we have discussed Python Program for Minimum Height of a Triangle with Given Base and Area
Given the base b of an isosceles triangle and a value m, the task is to find the count of the maximum number of squares of side length m that can be fitted inside the given isosceles triangle.

Formula:

(b / m – 1) * (b / m) / 2

where b is the base of an isosceles triangle.

m is the sidelength of the square.

Examples:

Example1:

Input:

Given base of triangle = 8
Given side of square = 3

Output:

The maximum number of squares with given sidelength that can be fitted inside the isosceles triangle = 
2

Example2:

Input:

Given base of triangle = 5
Given side of square =  2

Output:

The maximum number of squares with given sidelength that can be fitted inside the isosceles triangle = 
1

Program for Maximum Number of Squares that Can Fit in a Right Angle Isosceles Triangle in Python

Below are the ways to find the count of the maximum number of squares of side length m that can be fitted inside the given isosceles triangle.

• Using Mathematical Formula (Static Input)
• Using Mathematical Formula (User Input)

Method #1: Using Mathematical Formula (Static Input)

Approach:

• Give the base of the triangle as static input and store it in a variable.
• Give the side of the square as static input and store it in another variable.
• Create a function to say count_maximumsqures() which takes the given base of the isosceles triangle and side of the square as the arguments and returns the count of the maximum number of squares of the given sidelength required that can be fitted inside the given isosceles triangle.
• Inside the function, calculate the count of the maximum number of squares using the above mathematical formula and store it in a variable.
• Return the above count value.
• Pass the given base of the isosceles triangle and side of the square as the arguments to the count_maximumsqures() function, convert it into Integer using int() function, and print it.
• The Exit of the Program.

Below is the implementation:

# Create a function to say count_maximumsqures() which takes the given base of the
# isosceles triangle and side of the square as the arguments and returns the
# count of the maximum number of squares of the given sidelength required that
# can be fitted inside the given isosceles triangle.


def count_maximumsqures(gvn_base, squre_side):
    # Inside the function, calculate the count of the maximum number of squares using the
    # above mathematical formula and store it in a variable.
    cnt = (gvn_base / squre_side - 1) * (gvn_base / squre_side) / 2
    # Return the above count value.
    return cnt


# Give the base of the triangle as static input and store it in a variable.
gvn_base = 8
# Give the side of the square as static input and store it in another variable.
squre_side = 3
print("The maximum number of squares with given sidelength that can be fitted inside the isosceles triangle = ")
# Pass the given base of the isosceles triangle and side of the square as the arguments
# to the count_maximumsqures() function, convert it into Integer using int()
# function, and print it.
print(int(count_maximumsqures(gvn_base, squre_side)))

Output:

The maximum number of squares with given sidelength that can be fitted inside the isosceles triangle = 
2

Method #2: Using Mathematical Formula (User Input)

Approach:

• Give the base of the triangle as user input using the int(input()) function and store it in a variable.
• Give the side of the square as user input using the int(input()) function and store it in another variable.
• Create a function to say count_maximumsqures() which takes the given base of the isosceles triangle and side of the square as the arguments and returns the count of the maximum number of squares of the given sidelength required that can be fitted inside the given isosceles triangle.
• Inside the function, calculate the count of the maximum number of squares using the above mathematical formula and store it in a variable.
• Return the above count value.
• Pass the given base of the isosceles triangle and side of the square as the arguments to the count_maximumsqures() function, convert it into Integer using int() function, and print it.
• The Exit of the Program.

Below is the implementation:

# Create a function to say count_maximumsqures() which takes the given base of the
# isosceles triangle and side of the square as the arguments and returns the
# count of the maximum number of squares of the given sidelength required that
# can be fitted inside the given isosceles triangle.


def count_maximumsqures(gvn_base, squre_side):
    # Inside the function, calculate the count of the maximum number of squares using the
    # above mathematical formula and store it in a variable.
    cnt = (gvn_base / squre_side - 1) * (gvn_base / squre_side) / 2
    # Return the above count value.
    return cnt


# Give the base of the triangle as user input using the int(input()) function
# and store it in a variable.
gvn_base =  int(input("Enter some random number = "))
# Give the side of the square as user input using the int(input()) function and 
# store it in another variable.
squre_side =  int(input("Enter some random number = "))
print("The maximum number of squares with given sidelength that can be fitted inside the isosceles triangle = ")
# Pass the given base of the isosceles triangle and side of the square as the arguments
# to the count_maximumsqures() function, convert it into Integer using int()
# function, and print it.
print(int(count_maximumsqures(gvn_base, squre_side)))

Output:

Enter some random number = 5
Enter some random number = 2
The maximum number of squares with given sidelength that can be fitted inside the isosceles triangle = 
1

Explore more Example Python Programs with output and explanation and practice them for your interviews, assignments and stand out from the rest of the crowd.

• Python Program to Calculate Area and Perimeter of Equilateral Triangle
• Python Program to Calculate Volume of Dodecahedron
• Python Program to Calculate Volume and Surface Area of Hemisphere
• Python Program for Minimum Height of a Triangle with Given Base and Area